Pendahuluan
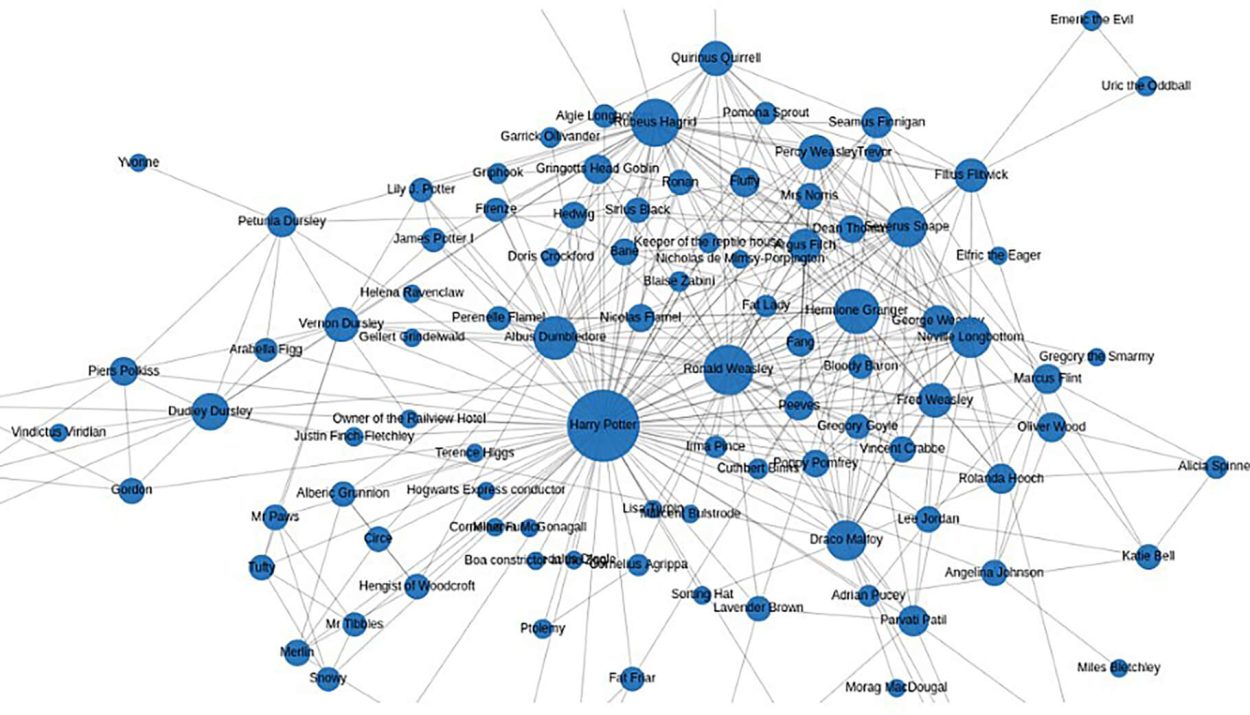
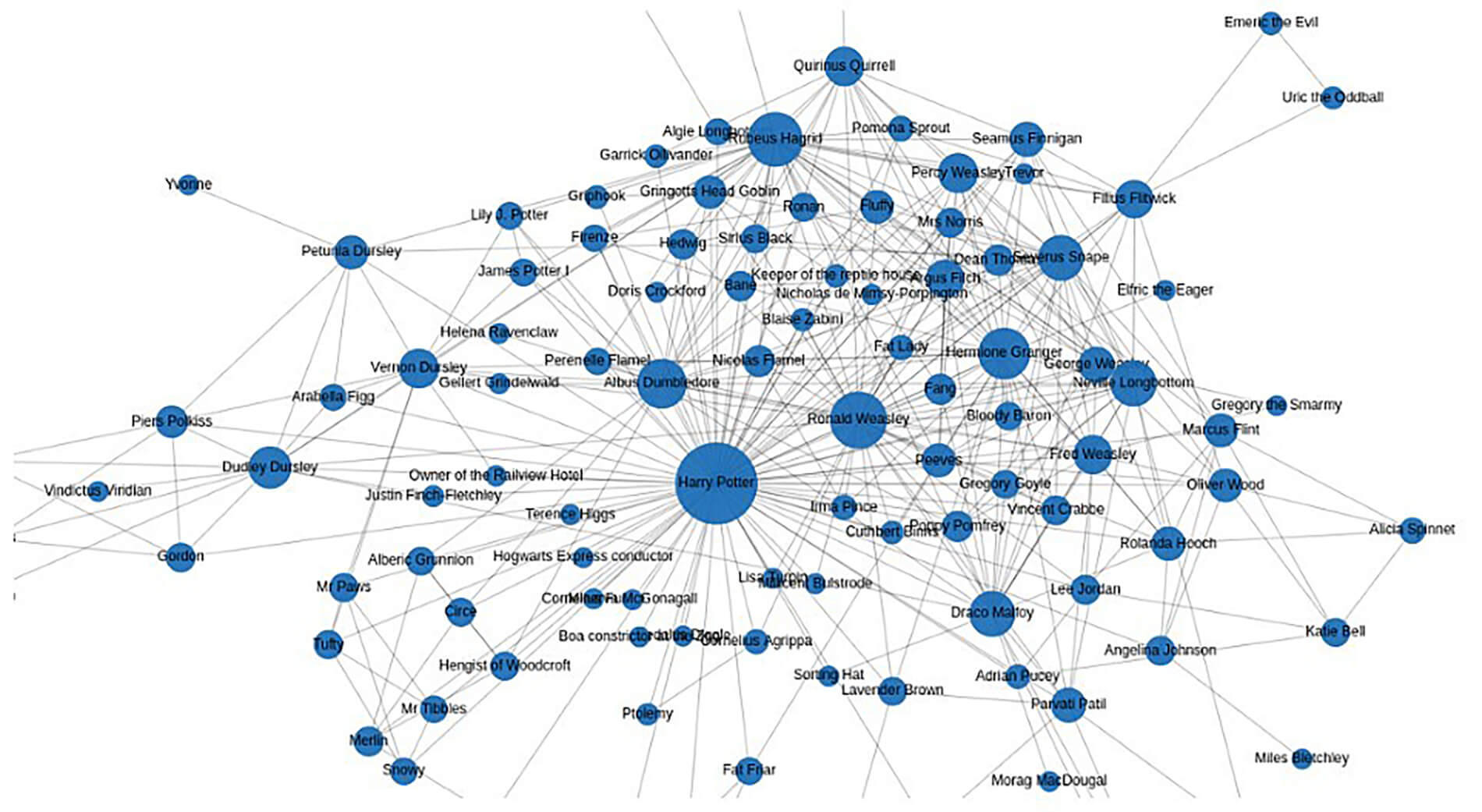
Graph Theory atau teori graf adalah cabang matematika yang mempelajari hubungan antara objek-objek dalam bentuk titik (node) dan garis (edge). Teori ini sangat penting karena banyak digunakan dalam berbagai bidang, seperti ilmu komputer, transportasi, jaringan sosial, hingga kecerdasan buatan.
Dalam kehidupan sehari-hari, kita sering menggunakan teori graf tanpa menyadarinya. Misalnya, saat mencari rute tercepat di Google Maps atau melihat rekomendasi teman di media sosial, di balik sistem tersebut ada algoritma yang bekerja berdasarkan teori graf.
Konsep Dasar dalam Graph Theory
Graf dan Komponennya
Graf terdiri dari dua komponen utama:
-
Simpul (Node/Vertex): Titik-titik yang mewakili objek.
-
Sisi (Edge): Garis yang menghubungkan simpul-simpul tersebut.
Jenis-jenis Graf
-
Graf tak berarah → Hubungan dua simpul tidak memiliki arah tertentu, misalnya jaringan pertemanan di media sosial.
-
Graf berarah → Setiap sisi memiliki arah tertentu, seperti jalur satu arah dalam peta.
-
Graf berbobot → Setiap sisi memiliki nilai tertentu, seperti jarak antara dua kota dalam peta navigasi.
-
Graf siklis dan asiklik → Graf siklis memiliki jalur melingkar, sedangkan graf asiklik tidak memiliki siklus.
Representasi Graf
-
Matriks Ketetanggaan → Representasi dalam bentuk tabel yang menunjukkan hubungan antar simpul.
-
Daftar Ketetanggaan → Representasi dalam bentuk daftar yang lebih efisien untuk graf besar.
Algoritma Penting dalam Teori Graf
1. Algoritma Pencarian Jalur Terpendek
-
Dijkstra’s Algorithm → Menentukan jalur terpendek dari satu titik ke titik lain.
-
Bellman-Ford Algorithm → Menangani graf dengan bobot negatif.
2. Algoritma Minimum Spanning Tree (MST)
-
Kruskal’s Algorithm → Membangun jaringan dengan biaya terendah, seperti dalam pembangunan jaringan listrik.
-
Prim’s Algorithm → Menentukan MST dengan cara menambahkan sisi satu per satu.
3. Algoritma Pencarian dalam Graf
-
Breadth-First Search (BFS) → Menelusuri simpul terdekat terlebih dahulu, berguna dalam pencarian jalur terpendek.
-
Depth-First Search (DFS) → Menelusuri simpul secara mendalam sebelum beralih ke yang lain, sering digunakan dalam problem pencarian solusi.
Aplikasi Graph Theory di Dunia Nyata
Teori graf memiliki banyak aplikasi di berbagai bidang:
-
Jaringan Komputer dan Internet
Digunakan untuk mengoptimalkan routing paket data di jaringan internet agar sampai ke tujuan dengan efisien. -
Analisis Media Sosial
Facebook, Instagram, dan Twitter menggunakan teori graf untuk menganalisis hubungan antar pengguna dan memberikan rekomendasi teman. -
Navigasi dan Transportasi
Google Maps menggunakan algoritma graf untuk mencari rute tercepat dari satu lokasi ke lokasi lain. -
Ilmu Bioinformatika
Teori graf membantu dalam menganalisis hubungan antara gen dan protein dalam tubuh manusia. -
Keamanan dan Kriptografi
Digunakan dalam pengamanan jaringan dan enkripsi data agar tidak mudah diretas.
Tantangan dan Perkembangan Terkini dalam Graph Theory
-
Kompleksitas Komputasi
Semakin besar jumlah simpul dan sisi dalam graf, semakin sulit komputasi yang diperlukan. -
Peran AI dan Machine Learning
Teori graf mulai diterapkan dalam AI untuk memahami pola hubungan antar data. -
Big Data dan Blockchain
Teknologi seperti blockchain juga menggunakan teori graf untuk mencatat transaksi dalam jaringan yang aman dan terdesentralisasi.
Kesimpulan
Teori graf adalah salah satu fondasi penting dalam dunia teknologi modern. Dengan berbagai algoritma dan aplikasinya, teori ini membantu kita dalam berbagai aspek kehidupan, mulai dari navigasi, analisis media sosial, hingga keamanan data.
Seiring perkembangan teknologi, teori graf akan terus berkembang dan berperan dalam inovasi masa depan. Bagi siapa saja yang tertarik dengan pemrograman dan matematika, memahami teori graf adalah langkah yang sangat berguna!